漸化式で解く [漸化式]
タイトルは、「続・給仕長帽子屋のたくらみ」というもので、
問題と解答(解説)は、それぞれ次のページにあります。
http://www.nikkei-science.com/page/magazine/alice/201506/question.html
http://www.nikkei-science.com/page/magazine/alice/201506/answer.html
この中で、作者(坂井公先生)は、「期待値を求める場合の常套手段」の「期待値の加法性」を用いて求めています。
残念ながら、私は、それを知らなかったので場合分けで求めました。
もちろん、52人の場合を、場合分けで求めるわけはなく、当然、漸化式を作って、n人の場合での場合分けを行ないます。
漸化式で解く場合は、「考え方」がすべてです。よい考え方が思い浮かぶと、簡単に漸化式が作れます。
下に示す3つの漸化式A(n),B(n),C(n)を用いれば、B(51)が求める答えとなります。
一人が座ったあとの状態で、その人のところで、机を開いて直線状にしたと考えましょう。その人は右のナプキンを取ったものとします。
A(n) は、空いた席が連続してn個ある場合で、かつ、どの席も両方のナプキンが残っている場合の犠牲者の期待値とします。
B(n) は、空いた席が連続してn個で、最初の席の左側のナプキンがなくて、それ以外の席は両方のナプキンが残っている場合の犠牲者の期待値とします。
C(n) は、空いた席が連続してn個で、最初の席の左側のナプキンがなくて、最後の席の右側のナプキンがなくて、それ以外の席は両方のナプキンが残っている場合の犠牲者の期待値とします。
まず、n=1,2の場合は、明らか、あるいは、場合分けで考えれば
A(1)=0, A(2)=0
B(1)=0, B(2)=1/4
C(1)=1, C(2)=1
となります。
なお、n=1のときには、すでに一人が座ったあとに1つ席が空いている場合なので、合計2人の場合のことです。n=2のときは、合計3人の場合のことです。
n>=3のときは、次の人がどの席に座るかで場合分けすると、右側と左側の状態をA(k),B(k),C(k), k<nで表わすことができます。それを足し合わせればA(n),B(n),C(n)での漸化式ができます。途中の場合分けの計算はすべて略しますが、結果として、
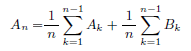
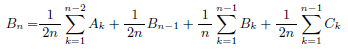
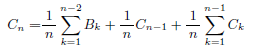
となります。
あとは、コンピュータを使って、多倍長有理数を扱える言語で、A(n),B(n),C(n)を求めていき、最終的にB(51)を求めます。
perlのbigratを使って求めた結果は次のとおりです。
97185682894552315055599361672425037016807
/17464044598281107886605680776556174847310
52427739679140223698377637888000000000000
およそ、6.4166となります。
数独を解く [DLX]
Algorithm XやDancing Linksの詳細は、ググればわかりやすい解説のページがでてきますので、割愛します。
また、数独をDLXで解く方法については、数独を「Exact Conver」問題として適用するのですが、これも割愛します。
Knuth先生の書かれたプログラムを実際に動かしてみましょう。
Knuth先生の書かれたプログラムは、以下のページにあります。
http://www-cs-faculty.stanford.edu/~uno/programs.html
この中から「DANCE」と「SUDOKU」のリンクでdance.w, sudoku.wをダウンロードします。
この.wの拡張子ですが、これはCWEBというものらしく、プログラムとドキュメントが一体化したものです。
ですので、コンパイルするには、ソースを取り出すプログラム(ctangle)が必要です。
ctangleは、livetexなどのパッケージに含まれているようです。他に、Knuth先生の次のページからソースをダウンロードできます。
http://www-cs-faculty.stanford.edu/~uno/cweb.html
通常のlinuxの環境では、次のコマンドでdance,sudokuのプログラムがビルドできます。
ctangle dance.w
make dance
ctangle sudoku.w
make sudoku
なお、ドキュメントは、PDFで見る場合は、
cweave dance.w
tex dance
dvipdf dance.dvi
のようになります。
さて、これをどう使うのでしょう?
数独の問題は、9x9のマスで構成されていますので、問題は、たとえば次のようになります。
これは、中央の9マスの数字を求める問題です。空欄は'.'として、9文字の9行で入力します。
123456789
456789123
789123456
234...891
567...234
891...567
345678912
678912345
912345678
これを次のコマンドラインに入力します。ファイルに書いておいて、リダイレクトするとよいでしょう。
ファイル名をprobremとしますと
./sudoku <probrem | ./dance 1
結果は次のように表示されます。
1:
p33 r35 c35 b45 (1 of 1)
p34 r36 c46 b46 (1 of 1)
p35 r37 c57 b47 (1 of 1)
p43 r48 c38 b48 (1 of 1)
p44 r49 c49 b49 (1 of 1)
p45 r41 c51 b41 (1 of 1)
p53 r52 c32 b42 (1 of 1)
p54 r53 c43 b43 (1 of 1)
p55 r54 c54 b44 (1 of 1)
Altogether 1 solutions, after 63 updates.
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
0 1 1 nodes, 7 updates
1 0 1 nodes, 7 updates
Total 10 nodes.
これではよく分からないですね。では、上記の結果を表示するプログラムをつくりましょう。
display_sudoku_dance_answer.plとします。以下のようなものです。
#!/usr/bin/perl
use strict;
my $inAns=0;
my @board=();
while(<>) {
my $lin=$_;
chomp $lin;
if ($inAns) {
if ($lin=~m{\s+([a-z]\d\d)\s+([a-z]\d\d)\s+([a-z]\d\d)\s+([a-z]\d\d)\s+}) {
# p13 r11 c31 b11 (1 of 1)
# r65 c05 b65 p60 (1 of 1)
my @col=($1,$2,$3,$4);
# find pXY
my ($x,$y)=(undef,undef);
my $dgt=undef;
for my $col (@col) {
if ($col=~m{p(\d)(\d)}) {
($y,$x)=($1,$2); # fixed bug
if (defined($dgt)) { last; }
next;
}
elsif ($col=~m{[a-z]\d(\d)}) {
$dgt=$1;
if (defined($x)) { last; }
next;
}
}
if (!defined($x)||!defined($dgt)) {
# error
print "ERROR: internal error.\n";
exit 1;
}
$board[$y][$x]=$dgt;
next;
}
else {
# disp answer
for (my $y=0; $y<9; $y++) {
for (my $x=0; $x<9; $x++) {
if (!defined($board[$y][$x])) {
print ".";
}
else {
print $board[$y][$x];
}
if ($x<8 && $x%3==2) {
print "|";
}
}
print "\n";
if ($y<8 && $y%3==2) {
print "---+---+---\n";
}
}
$inAns=0;
# thru to check ans number
}
}
if ($lin=~m{^\s*(\d+)\s*:}) {
# ans number
print "$lin\n";
$inAns=1;
next;
}
}
実行してみましょう。
./sudoku <probrem | ./dance 1 | ./display_sudoku_dance_answer.pl
結果は、次のようになります。
1:
...|...|...
...|...|...
...|...|...
---+---+---
...|567|...
...|891|...
...|234|...
---+---+---
...|...|...
...|...|...
...|...|...
では、少し考察してみましょう。
danceが出力した解の後ろに、どれだけ(大雑把に言うと)「手順」がかかったかが表示されています。
Altogether 1 solutions, after 63 updates.
このprogremでは63回の「手順」で全解(1個)が求まっています。
人が解いても簡単な問題ですね。
では、「世界一難しい」と銘打たれた数独の問題がどれだけ難しいかを、「手順」の数でみてみましょう。
「世界一難しい数独」でググると、2つの問題がヒットします。
ひとつは2010年のもの、もうひとつは2012年のものです。
それを入力してみると、「手順」は、
2010年の問題
Altogether 1 solutions, after 10676 updates.
2012年の問題
Altogether 1 solutions, after 50570 updates.
となりました。手順で5倍も大きいものとなっていますので、人が考える場合は5倍よりもかなり難しくなっているでしょう。
数独の難しさも「進化」していますね(^^)。
なお、DLXでの「手順」の数は、実は、同じ問題でも、問題の数値を入力する順序によってある程度変わってきます(変わらないこともあります)。
これは、dance.cでのbest_colの選択方法(同一のbest値があった場合の選択方法)によるためですが、興味ある方はAlgorithm Xの解説を調べてください。
(17-06-24追記)
x,yが入れ替わっていたバグがあったので修正しました。
穴の開いた六角形(その5) [ヘプティアモンド]
前回の続きです。
ギザギザな六角形が3種です。
<http://puzzler.sourceforge.net/docs/heptiamonds.html#hexagons>
Jagged hexagons (designs from Johannes H. Hindriks):
1.

719,972 Answers (considering rotations and reflections to be the same)
2.

30,511,236 Answers (considering rotations and reflections to be the same)
3.

431,567 Answers (considering rotations and reflections to be the same)
穴の開いた六角形(その4) [ヘプティアモンド]
前回の続きです。
次の5つ(13〜17番め)です。ここは、5つとも解が求まっています。
これで、穴の開いた六角形の17種は終了です。
<http://puzzler.sourceforge.net/docs/heptiamonds.html#hexagons>
Regular 12-unit-high (side length 6) hexagons with holes of various shapes & sizes:
13.

5,793 Answers (considering rotations and reflections to be the same)
14.

1,142 Answers (considering rotations and reflections to be the same)
15.

6,003 Answers (considering rotations and reflections to be the same)
16.

686 Answers (considering rotations and reflections to be the same)
17.

226,522 Answers (considering rotations and reflections to be the same)
次回は、ギザギザな六角形が3種です。
穴の開いた六角形(その3) [ヘプティアモンド]
前回の続きです。
次の4つ(9〜12番め)です。ここは、4つとも解が求まっています。
<http://puzzler.sourceforge.net/docs/heptiamonds.html#hexagons>
Regular 12-unit-high (side length 6) hexagons with holes of various shapes & sizes:
9.

17,056,347 Answers (considering rotations and reflections to be the same)
10.

35,623,320 Answers (considering rotations and reflections to be the same)
11.

599,652 Answers (considering rotations and reflections to be the same)
12.

121 Answers (considering rotations and reflections to be the same)
穴の開いた六角形(その2) [ヘプティアモンド]
前回の続きです。
次の4つ(5〜8番め)ですが、2つしか計算できていません。
特に、7番めのものは、非常に解が多く、全解を求めることはできないでしょう。
<http://puzzler.sourceforge.net/docs/heptiamonds.html#hexagons>
Regular 12-unit-high (side length 6) hexagons with holes of various shapes & sizes:
6.

25,446,444 Answers (considering rotations and reflections to be the same)
8.

15,959,858 Answers (considering rotations and reflections to be the same)
穴の開いた六角形(その1) [ヘプティアモンド]
穴の開いた六角形のその1です。
こちら<http://puzzler.sourceforge.net/docs/heptiamonds.html#hexagons>に、穴の開いた六角形が17種、他にギザギザな六角形が3種あります。
これから、何回かに分けて見ていきましょう。
<http://puzzler.sourceforge.net/docs/heptiamonds.html#hexagons>
Regular 12-unit-high (side length 6) hexagons with holes of various shapes & sizes:
まず、最初の4つですが、3つまでしか計算できていません。
1.
1,734,457 Answers (considering rotations and reflections to be the same)
2.
158,787,594 Answers (considering rotations and reflections to be the same)
3.
19,488,749 Answers (considering rotations and reflections to be the same)
結果が分かり次第、追加します。
最小高さの平行四辺形と未解決の問い2 [ヘプティアモンド]
台形と違って、平行四辺形の場合は最小の高さ3のものがあります。
これのコンピュータによる結果は
101,438 Answers (considering rotations and reflections to be the same)
です。
高さが最小の3だと解の数がかなり少ないようです。
さて、高さ3の台形が不可能であることは前々回に触れました。
しかし、たとえば、3つのユニットを足して、次のような形にすれば、「欠けた台形」になります。
これは
232,134 Answers (considering rotations and reflections to be the same)
となります。
では、例えば、下のように台形の中央部に「穴があいた台形」ではどうでしょうか?
穴の位置は、いずれも、台形の中央部(下の図の赤と緑の三角形があるところ)のどれかとします。
2つ、あるいは、3つが隣あって、穴が2つ、あるいは、1つでも構いません。
これをコンピュータで探索しているのですが、10%弱程度チェックが終了したものの、解が見つかっていません。
そこで、
未解決の問い 2:
上記の穴の空いた台形の解はいくつあるでしょうか? 解は存在しないのでしょうか?
解が存在しない場合、理由の簡単な説明ができるでしょうか?
これも結果が分かったときに報告します。
先に「理由の簡単な説明」が見つかれば、よいのですが…。
高さ4の平行四辺形と未解決の問い1 [ヘプティアモンド]
今回は、「未解決の問い 1」です。
前回の「高さ4の台形」を変形した「高さ4の平行四辺形」です。

まだこの全解は求められていません。おそらく4〜6ヶ月くらいかかるでしょう。
ということで、
未解決の問い 1: どちらがどれだけ解が多いでしょうか? またその理由は?
私の予想は次のとおり。
こちらの方が多い。ほとんど参考にならないが、穴あきの台形と平行四辺形の結果から。
はてさて、結果は如何に。
結果がわかったときには報告します。
一番高さの小さい台形 [ヘプティアモンド]
次はこの「形」です。
高さ3の台形は作れません(試してみればわかります。3ユニット余る/足りないのです)。
ですので、高さ4の台形が、台形で高さの一番小さいものとなります。
コンピュータによる結果は
2,058,918,339 Answers (considering rotations and reflections to be the same)
です。
これは実はとんでもない時間かかっています。分散処理して累計で約6.7年です。なので、解の数が間違っていたら目も当てられません(笑)。
次に背の高い台形は、高さが6となります。解の数はおそらくこの100〜1000倍くらいではないでしょうか。


